Le vulgarisateur et vidéaste Mr. Phi (qui est docteur en philosophie) a récemment fait une vidéo très complète (que je vous incite à voir) expliquant pourquoi il faut changer de mode de scrutin pour nos élections (notamment les présidentielles), et pourquoi le vote par approbation semble être un choix approprié pour remplacer le mode de scrutin actuel.
Très rapidement, notre mode de scrutin actuel pour les présidentielles en France, appelé "vote uninominal à deux tours" consiste à voter pour au plus un candidat au premier tour, puis les deux candidats ayant le plus haut score vont au second tour. Dans un "vote par approbation", chaque électeur inscrit sur son bulletin les noms de tous les candidats qu'il approuve (donc autant qu'il le souhaite) et le candidat ayant le plus de voix, étant celui qui est approuvé par le plus grand nombre d'électeurs, remporte l'élection.
Notez que si vous avez manqué ce sondage, le CNRS et de nombreux laboratoires français (Université de Caen, CREM. Paris School of Economics. Université Jean-Monnet Saint-Étienne, GATE. Université de Strasbourg, BETA. Université Grenoble-Alpes, Grenoble-INP, LIG.) ont lancé une expérimentation dans laquelle ils testent une grande variété de mode de scrutin, incluant le vote par approbation, le jugement majoritaire, le vote par score et des méthodes de vote par classement. Vous pouvez participer en 5 minutes en suivant ce lien vote.imag.fr.
Le sondage
A la fin de sa vidéo, Mr. Phi a proposé à ses abonnés de répondre à un sondage dans lequel ils pouvaient dire quel serait leur bulletin si l'élection suivait le vote par approbation. Il a également demandé quel était le vote des participants à l'élection présidentielle en cours, ce qui nous sera utile pour débiaiser en partie les résultats. Je lui ai proposé d'analyser les résultats de ce sondage.
Au final, le jeu de données contient 6801 réponses, ce qui est très conséquent pour un jeu de données de vote par approbation. Le graphique suivant montre les résultats bruts du sondage, c'est-à-dire pour chaque candidat, le pourcentage de participants qui approuvent ce candidat, et le pourcentage de participants qui ont voté pour ce candidat à l'élection.
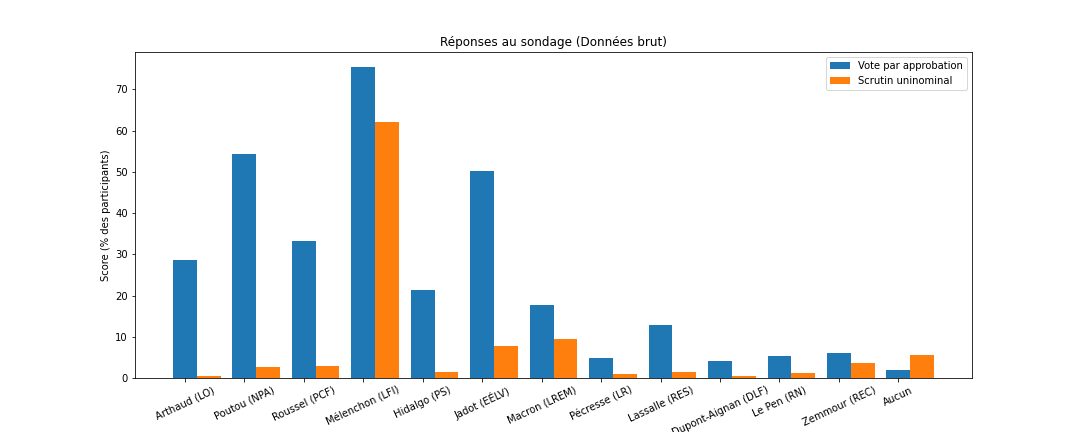
En prenant les données brutes, Mélenchon obtiendrait le meilleur score par approbation. Mais attention, c'est aussi celui qui reçoit le plus de vote à l'élection officielle parmi les participants aux sondages, on ne peut donc pas prendre ces données telles quelles. En effet, si on compare le score des candidats à l'élection parmi les participants au sondage et leurs scores réels à l'élection, on obtient le graphique suivant, dans lequel la gauche est sur-représentée.
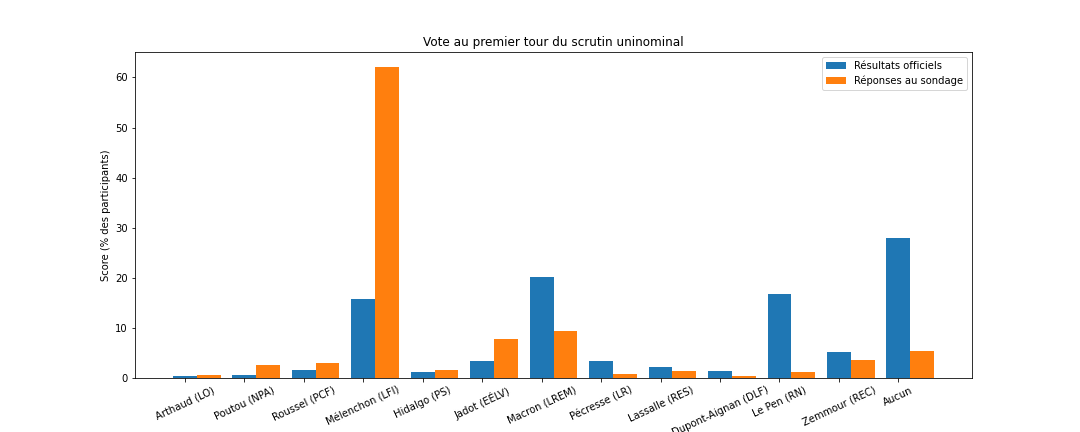
On constate notamment que 60% des participants au sondage votent Jean-Luc Mélenchon. On peut alors débiaiser en partie les résultats en assignant un poids à chaque participant. Les participants dont le candidat est sur-représenté (tous ceux qui sont à gauche de Jadot) auront un poids inférieur à 1, et tous les autres un poids supérieur à 1. Pour cela, j'ai enlevé les votes blancs et nuls ainsi que les abstentionnistes, et je n'ai pas pris en compte les participants au sondage déclarant ne voter pour aucun candidat à l'élection et le poids d'un candidat est égal à son score officiel divisé par son score dans le sondage. Par exemple, un électeur de Mélenchon aura un poids de 0.33 tandis qu'un électeur de Marine Le Pen sera compté environ 17 fois.
Cette étape permet de réduire le biais dans les résultats, mais elle est évidemment très loin d'être parfaite, car elle ne prend pas en compte les facteurs socio-démographiques (âge, profession, etc.) qui sont normalement utilisé par les instituts de sondage. Il faut donc prendre les résultats qui vont suivre avec des pincettes, et toujours considérer qu'il y a une marge d'erreur énorme. En prenant en compte les biais, on obtient le graphique suivant :
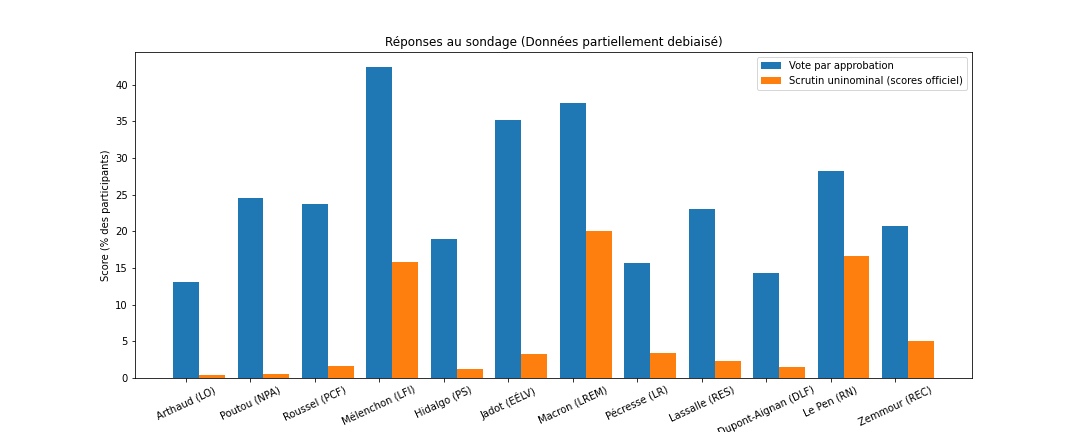
Tout d'abord, on constate que tous les candidats sont approuvés par au moins 10% de l'électorat. Il est évident que chaque candidat augmente son score puisque les participants peuvent mettre plusieurs noms dans l'urne, contre un seul nom pour le scrutin uninominal. Sur ce graphique, Jean-Luc Mélenchon arrive toujours en tête, suivi de Emmanuel Macron et de Yannick Jadot. Marine Lepen arrive 4e.
Correlation entre candidats
Grâce à ce jeu de données, on peut aussi regarder à quel point deux candidats sont proches en se basant sur leur électorat. On construit une matrice de corrélation dans laquelle la proximité entre deux candidats est calculée grâce à l'indice de Jacquard (Vous pouvez cliquer sur le lien Wikipédia pour en savoir plus). On obtient alors la matrice de corrélation suivante:
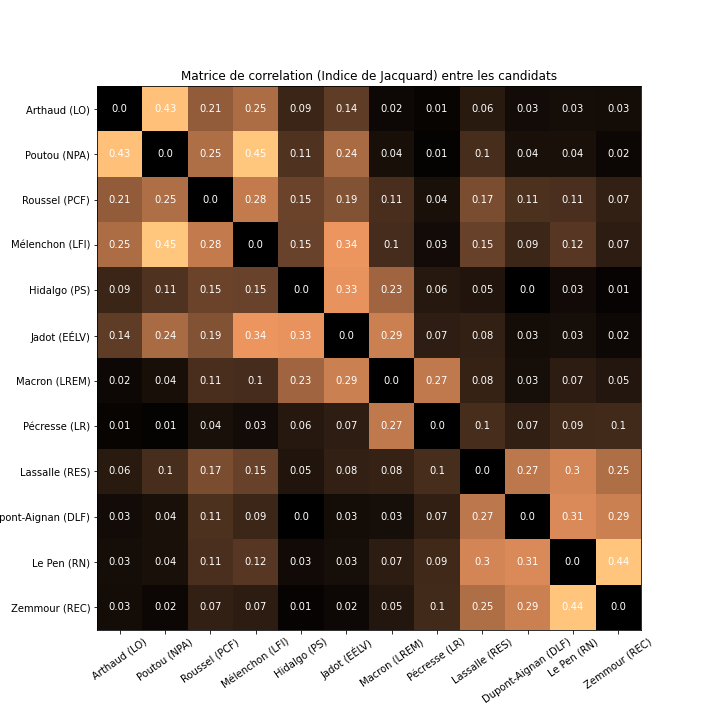
On observe sans surprise que les candidats classés à gauche sont proches, et que les candidats classés à l'extrême-droite sont proches. Une matrice comme ça étant peu lisible, je vous propose la même chose sous forme de graphe. Un lien entre deux candidats signifie que leur indice de jacquard est plus grand que 0.1. Plus le candidat est gros, plus son score est haut.
Nombre d'approbations
Enfin, ce jeu de données nous permet d'analyser le nombre d'approbations moyenne par participants. Celui-ci se situe entre 3 et 4, avec la distribution suivante :
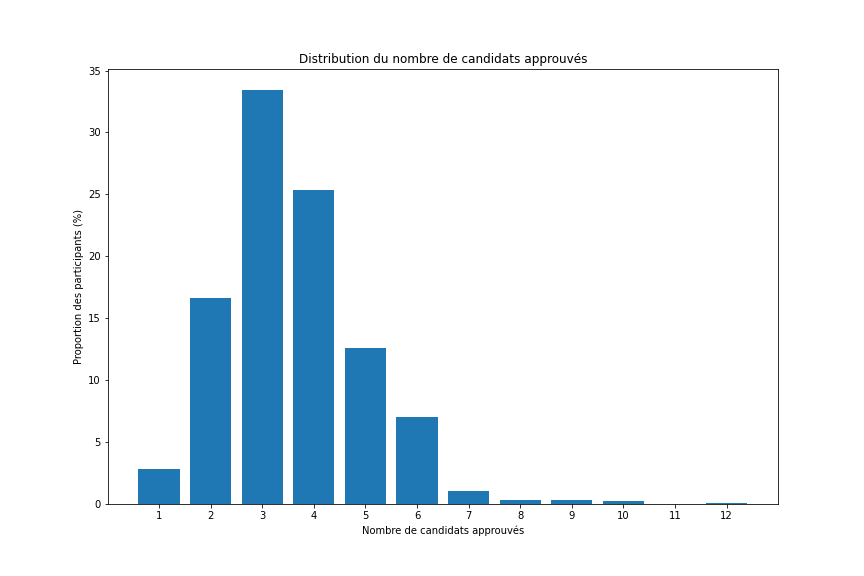
Si on observe l'électorat de chaque candidat à l'élection officielle, on peut voir quelques différences dans le nombre d'approbation, par exemple Eric Zemmour est le candidat pour lequel le moins d'électeurs sont prêts à approuver un autre candidat que lui (suivi par Emmanuel Macron).
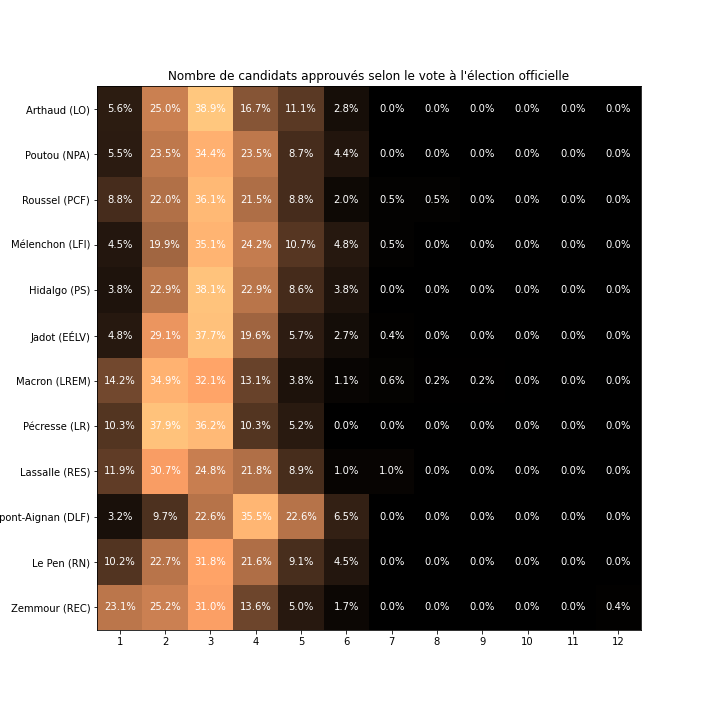
On peut faire le même graphique mais pour chaque candidat, on se base sur les participants ayant approuvé ce candidat, et non ceux qui ont voté pour lui à l'élection officielle.
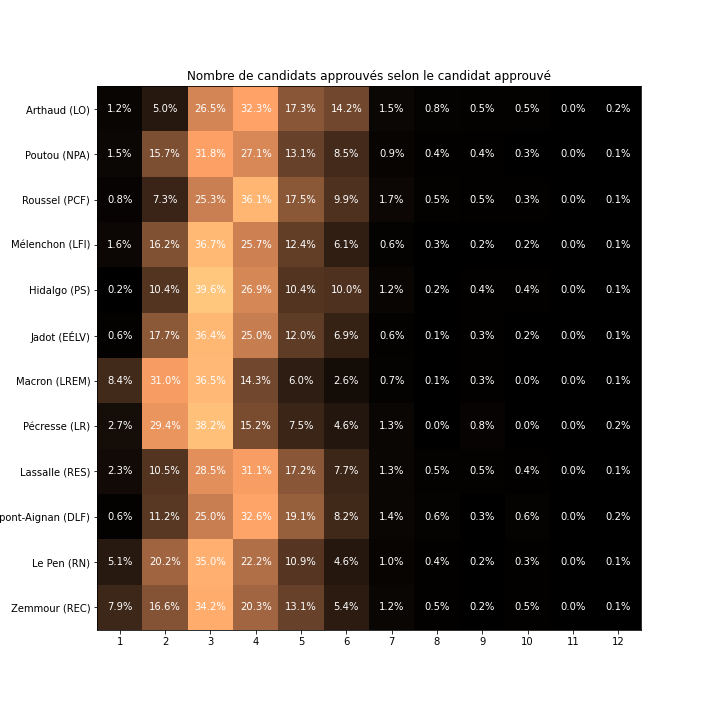
Autres remarques
Il existe une variante du vote par approbation qui se déroule en deux tours. Au premier tour, on vote par approbation, et deux candidats sont sélectionnés pour accéder au second tour. La question est alors, quels candidats selectionner ? Une réponse naturelle serait de choisir les deux candidats ayant le plus grand nombre d'approbations. Mais cela pose problème. Imaginons que Emmanuel Macron obtient le nombre d'approbation le plus grand et qu'il possède un clone parfait de Emmanuel Macron qui se présente avec le même programme que lui, à tel point que les gens qui approuvent le clone sont exactement ceux qui ont approuvé l'original. Alors les deux finalistes seront Macron et son clone, et le débat de l'entre-deux tours risque de ne pas être très intéressant. Une solution à ça serait de sélectionner tout d'abord le candidat ayant le plus grand nombre d'approbations, puis d'enlever tous les électeurs ayant approuvé ce candidat, et enfin choisir comme second finaliste le candidat ayant le plus grand nombre d'approbations parmi les électeurs restants. Comme ça, plus de problèmes de clones. Cela soulève cependant d'autres problèmes, notamment le retour du vote purement stratégique, qui avait disparu avec le vote par approbation.
En réalité, il existe une grande variété de règles possibles pour le mode de scrutin par approbation à deux tours. Vous pouvez en trouver une analyse dans l'article scientifique Approval with Runoff que j'ai co-écrit avec Jérôme Lang, Remzi Sanver et Jean-François Laslier.
Dans le cas de ce sondage, le résultats sont les mêmes pour chaque règles de vote: Les deux finalistes sont Jean-Luc Mélenchon et Emmanuel Macron.